 |
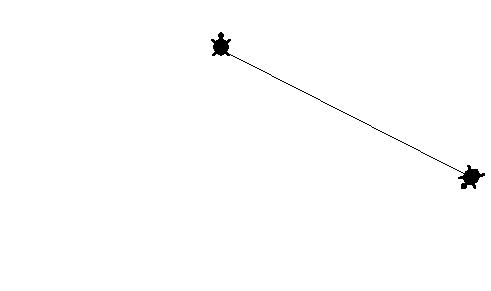
 重りをカメにしたら、どうなるかな? 重りをカメにしたら、どうなるかな? カメの カメの |
||
|
|||
| 1.振り子のもと を左クックして開いて、プログラミングを始めましょう。 |
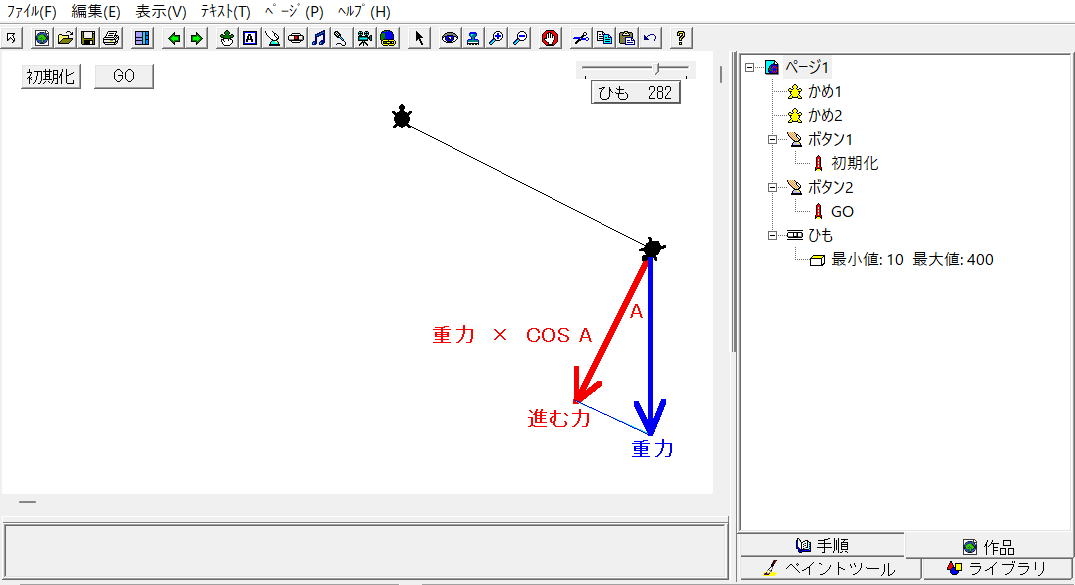 |
| 2.振り子のゆれをプログラミングします。 | |||
| ・重りの進む力で、だんだん速くなる運動を考えます。 ・重りの進む力は、 重力 × ・計算値の
|
|||
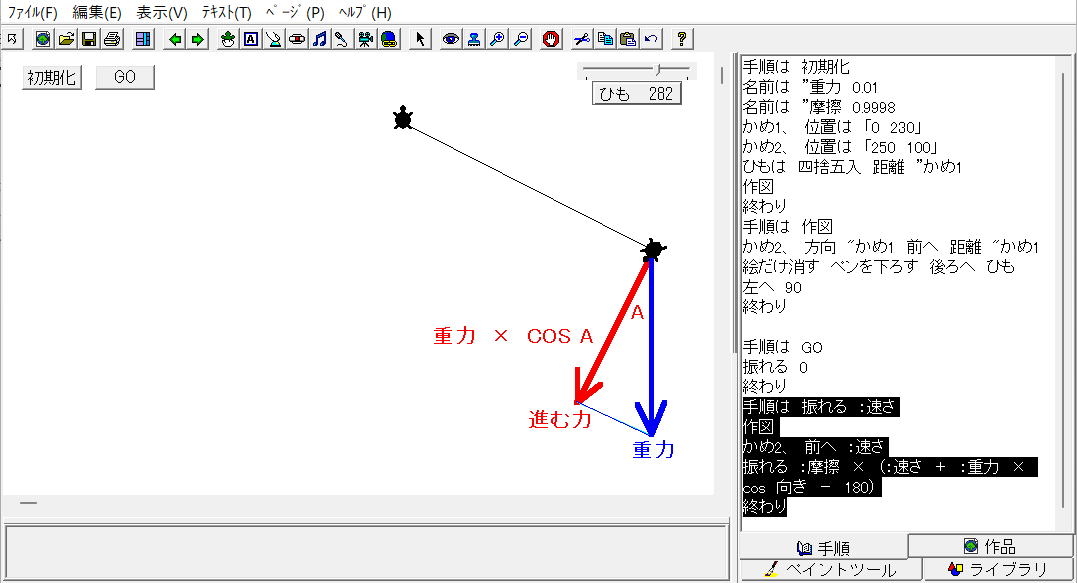 |
| ・ ・ ・ |
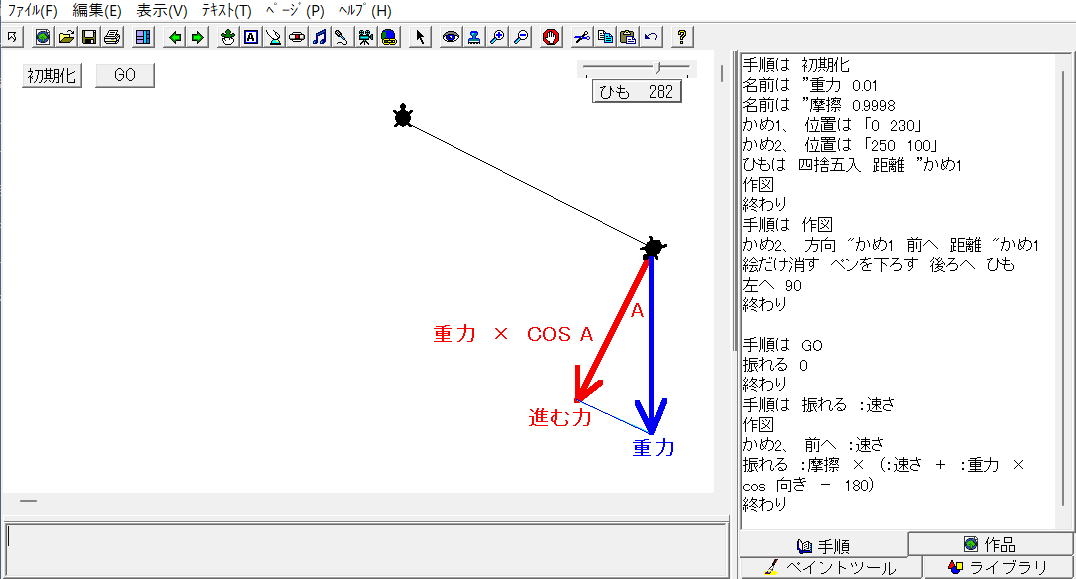 |
| ・振り子のような |
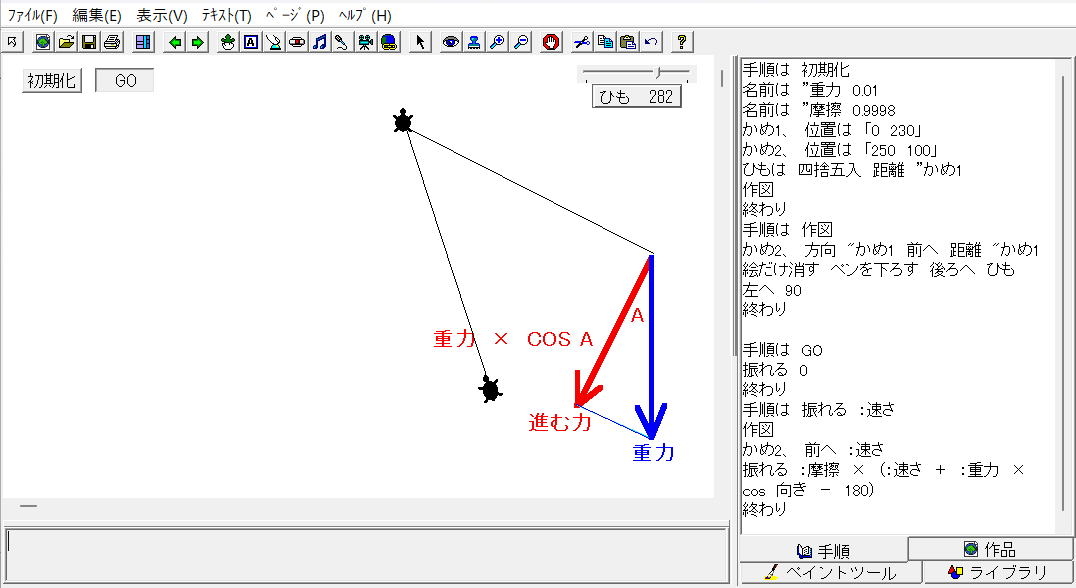 |
| ・ |
| ---三角関数--- |
 |
 重りをカメにしたら、どうなるかな? 重りをカメにしたら、どうなるかな? カメの カメの |
||
|
|||
| 1.振り子のもと を左クックして開いて、プログラミングを始めましょう。 |
 |
| 2.振り子のゆれをプログラミングします。 | |||
| ・重りの進む力で、だんだん速くなる運動を考えます。 ・重りの進む力は、 重力 × ・計算値の
|
|||
 |
| ・ ・ ・ |
 |
| ・振り子のような |
 |
| ・ |